작성일자 글쓴이 penta

Physics, 그런데 이제 Sling-shot을 곁들인。

\text{Constants}\\ C_d=0.47\, \text{공의 항력계수}\\ \rho=1.293 [kgm^{-3}]\, \text{공기의 밀도, 1기압, 섭씨 25도}\\ D=8730 [kgm^{-3}]\, \text{Brass, 섭씨 0도}// \text{Physical Variables}\\ L_t=0.7 [m]\, \text{잡아당기는 거리}\\ t_r=0.15 [s]\, \text{반응속도, 프로게이머 기준}\\ V_c=100 [ms^{-1}]\, \text{눈을 관통하기 위한 접촉 시점의 요구 속력}\\ r_e=0.012 [m]\, \text{안구의 반지름}\\ r_b=r_e\, \text{공의 반지름}
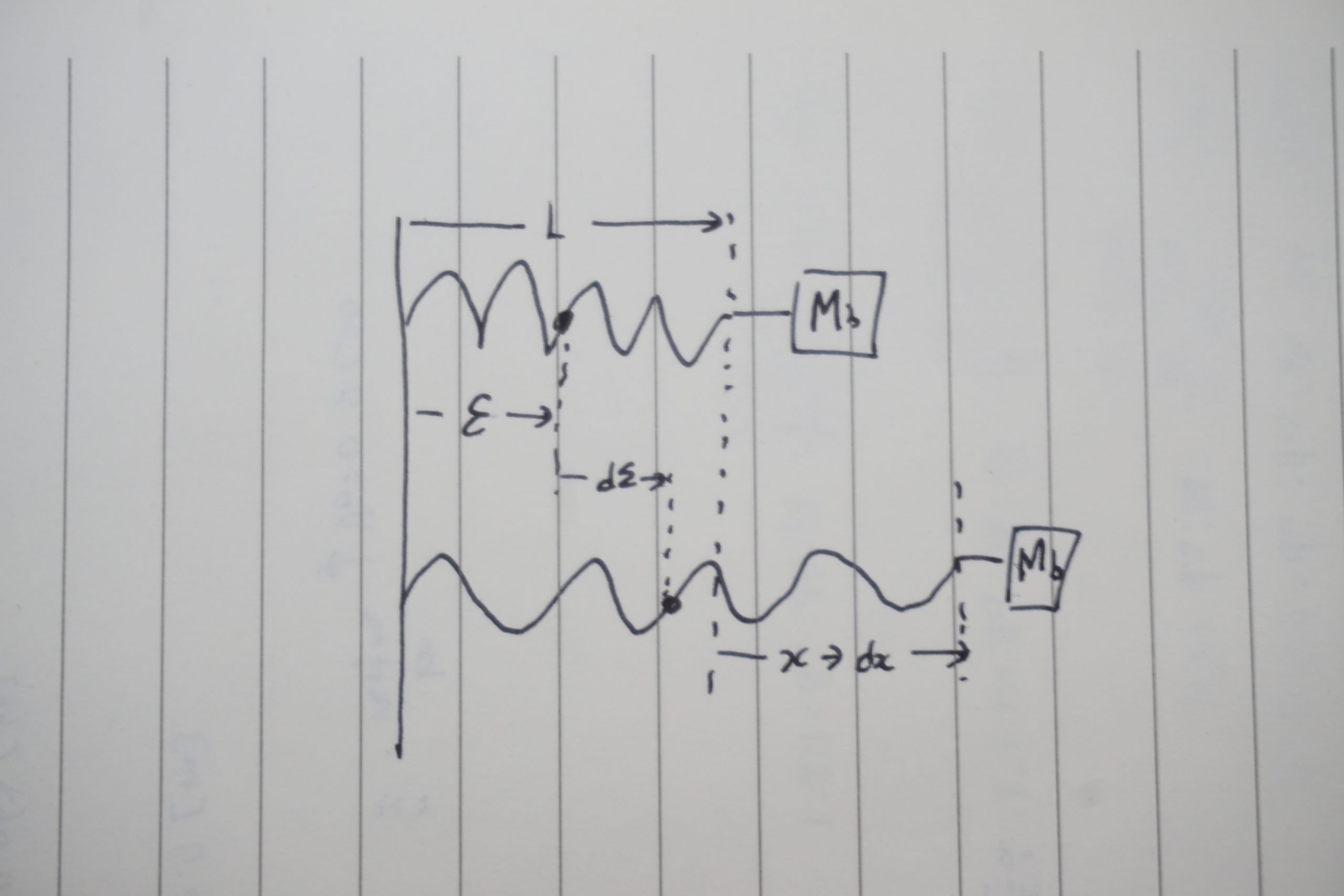
\text{Equations}\\ \text{새총 방정식}\\ \varepsilon =\frac{L}{2} \; \therefore \frac{d\varepsilon}{\varepsilon}=\frac{x}{L}=\frac{dx}{L} \quad d\varepsilon=\frac{\varepsilon}{L} dx \qquad \dot{\varepsilon} = \frac{\varepsilon}{L} \dot{x} \\ E^k_b=\frac{1}{2} M_b \dot{x}^2 \\ E^k_s=\frac{1}{2} \int_0^L \sigma d\varepsilon \left( \frac{\varepsilon}{L} \dot{x} \right) ^2 \, dx=\frac{1}{6} \sigma L \dot{x}^2=\frac{1}{6}M_b \dot{x}^2\\ E^k = \frac{1}{2} \left( M_b + \frac{1}{3} M_s \right) \dot{x}^2\\ E^p=\frac{1}{2}kx^2\\ E=\frac{1}{2} \left( M_b + \frac{1}{3} M_s \right) \dot{x}^2 + \frac{1}{2} k x^2\\ \frac{dE}{dx} = 0 =\frac{d}{dx} \left\{ \left( \frac{1}{2} M_b+\frac{1}{6} M_s \right) \dot{x}^2 + \frac{1}{2} k x^2 \right\} = \left( M_b+ \frac{1}{3} M_s \right) \ddot{x} + kx \qquad \ddot{x}=\frac{kx}{M_b + \frac{1}{3} M_s } \\ v = \int_0^t \ddot{x} \, dx = \frac{k}{M_b+\frac{1}{3} M_s} \cdot \frac{1}{2} t^2 \\ \text{항력 방정식}\\ F_A=-\frac{1}{2}C_d \rho A_b v^2\\ a_A= -\frac{-3 C_d \rho }{8Dr} v^2\\ \dot{x} = \int_0^T - \frac{3 C_d \rho }{8Dr} \dot{x}^2 t dt + v_0 =-\frac{3 C_d \rho }{8Dr} \dot{x}^2 +v_0 \\ v_0 = \frac{3 C_d \rho }{8Dr} v^2 + v

답글 남기기

이메일 주소는 공개되지 않습니다. 필수 필드는 *로 표시됩니다

이 사이트는 스팸을 줄이는 아키스밋을 사용합니다. 댓글이 어떻게 처리되는지 알아보십시오.