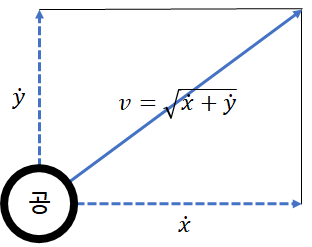
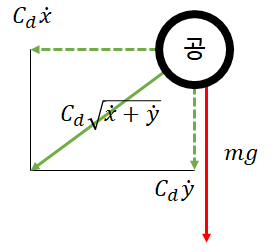
속도 Domain 힘 Domain 투사체 질량 m F=-C_d v=-C_d \sqrt{\dot{x}+\dot{y} } v=v_0, θ=θ_0
m \ddot{x}+C_d \dot{x} =0 m \ddot{y}+C_d \dot{y} =-mg
m \ddot{x}+C_d \dot{x} =0
특성방정식 m \lambda ^2+C_d \lambda =0 \lambda =0, -C_d/m
x(t)=c_1 e^0+c_2 e^{- \frac{C_d}{m} t}=c_1+c_2 e^{- \frac{C_d}{m} t}
초기조건x'(t)=c_2 {- \frac{C_d}{m}} e^{-\frac{C_d}{m} t} x'(0)=v_0 cos(θ_0), x_0=0
c_2=- \frac{m}{C_d} v_0 \cos{θ_0}, c_1=\frac{m}{C_d} v_0 \cos{θ_0}
x(t)=\frac{m}{C_d} v_0 \cos{θ_0 } - \frac{m}{C_d} v_0 \cos{θ_0 } \cdot e^{- \frac{C_d}{m} t}
my C_d \ddot{y}=-mg=r(t)
r(t)=0 으로 놓고 제차 상미방으로 풀이
특성방정식 m \lambda^2+C_d \lambda=0
\lambda=0, -\frac{C_d}{m}
y_h (t)=c_1 e^0+c_2 e^{-\frac{C_d}{m} t}=c_1+c_2 e^(-\frac{C_d}{m} t)
y_h (t)=\frac{m}{C_d} v_0 \sin{θ_0}-(\frac{m}{C_d} v_0 \sin{θ_0}+(m^2 g)/C_d ) \cdot e^{-\frac{C_d}{m} t}
r(t)=-mg=k 꼴이므로 y_p (t)=A 로 놓으면 답이 안 나옴y_p (t)=Ax+B 라고 하자
C_d \cdot (A)=-mg, B=\frac{m^2 g}{{C_d}^2}
y_h (t)=\frac{m}{C_d} v_0 \sin{θ_0}- (\frac{m}{C_d} v_0 \sin{θ_0}+\frac{m^2 g}{C_d} ) \cdot e^{-\frac{C_d}{m} t} y_p (t)=-\frac{mg}{C_d} t+\frac{m^2 g}{{C_d}^2}
y(t)=\frac{m}{C_d} v_0 \sin(θ_0)-(\frac{m}{C_d} v_0 \sin(θ_0)+(m^2 g)/C_d ) \cdot e^{-\frac{C_d}{m} t} -\frac{mg}{C_d} t+\frac{m^2 g}{{C_d}^2}
import math
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import (MultipleLocator, AutoMinorLocator)
v0 = 100.0 # m/s
#a0 # rad
m = 1.0 # kg
#Cd # kg/s
g = 9.8 # m/s^2
cond = [(1/3 * math.pi, 0.1), (1/4 * math.pi, 0.1), (1/6 * math.pi, 0.1)] # (a0, Cd)
dt = 0.001 # s
def doit(a0, Cd):
t = [0.0]
x = [0.0]
y = [0.0]
while y[-1] >= 0.0:
t.append(t[-1] + dt)
ex = math.exp(-Cd / m * t[-1])
x.append(
m / Cd * v0 * math.cos(a0)
- m / Cd * v0 * math.cos(a0) * ex
)
y.append(
m / Cd * v0 * math.sin(a0)
- (m / Cd * v0 * math.sin(a0) + m**2 * g / Cd**2) * ex
- m * g / Cd * t[-1]
+ m**2 * g / Cd**2
)
return (x, y)
leg = []
fig, ax = plt.subplots()
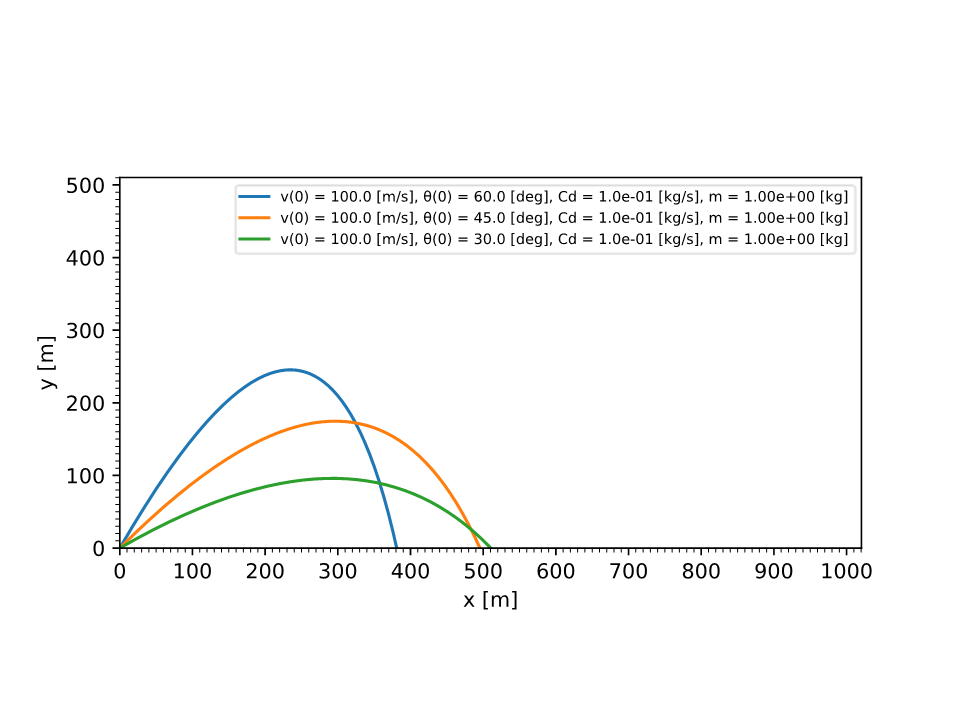
for a0, Cd in cond:
(x, y) = doit(a0, Cd)
ax.plot(x, y)
leg.append(f"v(0) = {v0:.1f} [m/s], θ(0) = {a0/math.pi*180.0:.1f} [deg], Cd = {Cd:.1e} [kg/s], m = {m:.2e} [kg]")
plt.xlim(0.0, v0**2 / g)
plt.ylim(0.0, v0**2 / g / 2)
plt.xlabel("x [m]")
plt.ylabel("y [m]")
plt.gca().set_aspect('equal', 'box')
plt.legend(leg, fontsize="x-small")
ax.xaxis.set_major_locator(MultipleLocator(100))
ax.xaxis.set_major_formatter('{x:.0f}')
ax.xaxis.set_minor_locator(MultipleLocator(10))
ax.yaxis.set_major_locator(MultipleLocator(100))
ax.yaxis.set_major_formatter('{x:.0f}')
ax.yaxis.set_minor_locator(MultipleLocator(10))
plt.savefig('posplot.svg', transparent=True)
import math
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import (MultipleLocator, AutoMinorLocator)
v0 = 100.0 # m/s
a0 = 5/12 * math.pi # rad
m = 0.15 # kg
Cd = 0.1 # kg/s
g = 9.8 # m/s^2
dt = 0.001 # s
def doit(a0, Cd):
t = [0.0]
vx = [0.0]
vy = [0.0]
y = 0.0
while y >= 0.0:
t.append(t[-1] + dt)
vx.append(
v0 * math.cos(a0) * math.exp(-Cd / m * t[-1])
)
vy.append(abs(
(v0 * math.sin(a0) + m * g / Cd) * math.exp(-Cd / m * t[-1])
- m * g / Cd
))
y = m / Cd * v0 * math.sin(a0) \
- (m / Cd * v0 * math.sin(a0) + m**2 * g / Cd**2) * math.exp(-Cd / m * t[-1]) \
- m * g / Cd * t[-1] \
+ m**2 * g / Cd**2
return (t, vx, vy)
leg = []
fig, ax = plt.subplots()
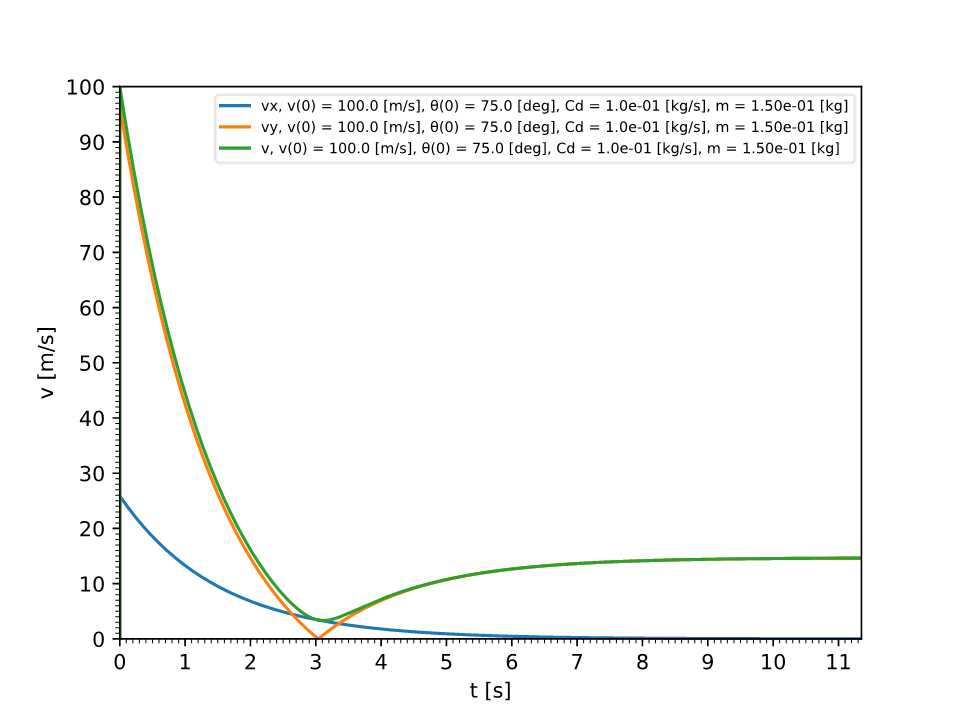
(t, vx, vy) = doit(a0, Cd)
ax.plot(t, vx)
ax.plot(t, vy)
vt = []
for va, vb in zip(vx, vy):
vt.append(math.sqrt(va ** 2 + vb ** 2))
ax.plot(t, vt)
leg.append(f"vx, v(0) = {v0:.1f} [m/s], θ(0) = {a0/math.pi*180.0:.1f} [deg], Cd = {Cd:.1e} [kg/s], m = {m:.2e} [kg]")
leg.append(f"vy, v(0) = {v0:.1f} [m/s], θ(0) = {a0/math.pi*180.0:.1f} [deg], Cd = {Cd:.1e} [kg/s], m = {m:.2e} [kg]")
leg.append(f"v, v(0) = {v0:.1f} [m/s], θ(0) = {a0/math.pi*180.0:.1f} [deg], Cd = {Cd:.1e} [kg/s], m = {m:.2e} [kg]")
plt.xlim(0.0, t[-1])
plt.ylim(0.0, v0)
plt.xlabel("t [s]")
plt.ylabel("v [m/s]")
#plt.gca().set_aspect('equal', 'box')
plt.legend(leg, fontsize="x-small")
ax.xaxis.set_major_locator(MultipleLocator(1))
ax.xaxis.set_major_formatter('{x:.0f}')
ax.xaxis.set_minor_locator(MultipleLocator(0.1))
ax.yaxis.set_major_locator(MultipleLocator(10))
ax.yaxis.set_major_formatter('{x:.0f}')
ax.yaxis.set_minor_locator(MultipleLocator(1))
plt.savefig('velplot2.svg', transparent=True)